C++ 动态规划 学习记录

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

维基百科zh.wikipedia.org/wiki/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92

感觉维基给的定义有点抽象……？说简单点就是：

1. 把原来问题拆成小问题。
2. 逐个求解小问题，然后把答案保存起来。
3. 再根据小问题的答案去反推原来问题的题解。

核心就是：拆分子问题，记住答案，以减少重复的计算。

感觉还是看不懂……用网上一个很流行的例子去解释：

A ： “1+1+1+1+1+1+1+1 =？”
A ： “上面等式的值是多少”
B ： “8”
A : 在上面等式的左边写上 “1+” 呢？
A : “此时等式的值为多少”
B : 很快得出答案 “9”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”

也就是说我想办法记住过去的答案，这样我不用重复计算了。

两种形式

求解的方式有两种：自顶向下的备忘录法、自底向上。

举个例子：斐波那契数列。也就是说：

$Fib(0)=1\$
Fib(1)=1\
Fib(n)=Fib(n-1)+Fib(n-2)\

这个用递归可以直接解决：

int fib(int n){
    if(n==0)return 1;
    if(n==1)return 1;
    if(n>=2)return fib(n-1)+fib(n-2);
}

假设我输入 6，那么执行的递归树是这样：

graph TD;

A["fib(6)"]-->B["fib(5)"]-->C2["fib(4)"]-->D3["fib(3)"]-->E4["fib(2)"]-->F5["fib(1)"];
A-->C1["fib(4)"]-->D1["fib(3)"]-->E3["fib(2)"]-->F4["fib(1)"];
B-->D2["fib(3)"]-->E2["fib(2)"]-->F3["fib(1)"];
C1-->E1["fib(2)"]-->F1["fib(1)"];
D1-->F2["fib(1)"];
E1-->G1["fib(0)"];
C2-->D4["fib(2)"]-->E5["fib(1)"];
D2-->E6["fib(1)"];
D3-->E7["fib(1)"];
D4-->F6["fib(0)"];
E2-->F8["fib(0)"];
E3-->F7["fib(0)"];
E4-->F9["fib(0)"]; 

从上面的递归树中可以看到，我运行一个 fib(6)，很多重复的节点，比如 fib(5)、fib(2)等等，被重复执行了很多次，这样的结果就是浪费时间。
这些重复的节点我们可以在遇到、计算之后，将其记录下来，后面再使用的时候直接把结果拉过来用，这样就节省了大量的时间。

我们分别用自顶向下和自底向上的方法，去解决斐波那契数列问题。

自顶向下的备忘录法

int memo[n]={-1};

int fib(int n,int memo[]){
    if(memo[n]!=-1)return memo[n];
    if(n<=2)memo[n]=1;
    else memo[n]=fib(n-1,memo)+fib(n-2,memo);
    return memo[n];
}

备忘录法还是比较好理解的，先创建一个数组 memo 用来存储每个斐波那契数列对应的每一个值，然后再递归的时候，如果发现 memo 中存在之前已经计算好的值，则直接调用；如果还没有算过，则计算后保存在 memo 数组中。这样第n此计算 fib 时就不用重新递归了，效率大大提高。

自底向上

备忘录法减少了重复的计算，但无论怎样，计算时还是递归去算的，既然我 fib(1)、fib(2)这样的都要算，那我为什么不先算好 fib(1)、fib(2)呢？

如果我从 fib(1) fib(2)开始，往上计算到目标的 fib（比如 fib(6)），这就是自底向上的动态规划，这种方法也是动态规划的核心：先计算子问题，再由子问题计算父问题。

int fib(int n){
  int memo[n];
  memo[0]=0;
  memo[1]=1;
  for(int i=2;i<=n;++i){
    memo[i]=memo[i-1]+memo[i-2];
}
    return memo[n];
}

自底向上的计算方法，避免了递归产生的较高的栈开销，进一步降低了空间复杂度。（正常人类手算也是这么算的吧）

由于实际参与循环的只有数组中的三个变量，如果中间计算的结果我们都不需要，那么我们还可以用三个变量代替整个数组，进一步压缩空间。

那么优化之后的代码应该是这样：

int fib(int n){
  int memo[3]={1,1,0};
  if(n<=1)return n;
  for(int i=2;i<=n;++i){
    memo[0]=memo[2]+memo[1];
    memo[2]=memo[1];
    memo[1]=memo[0];
  }
  return memo[0];
}

这就是一个非常简单的动态规划。

例题

P1002 [NOIP2002 普及组] 过河卒

（如有侵权请联系我删除）

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。

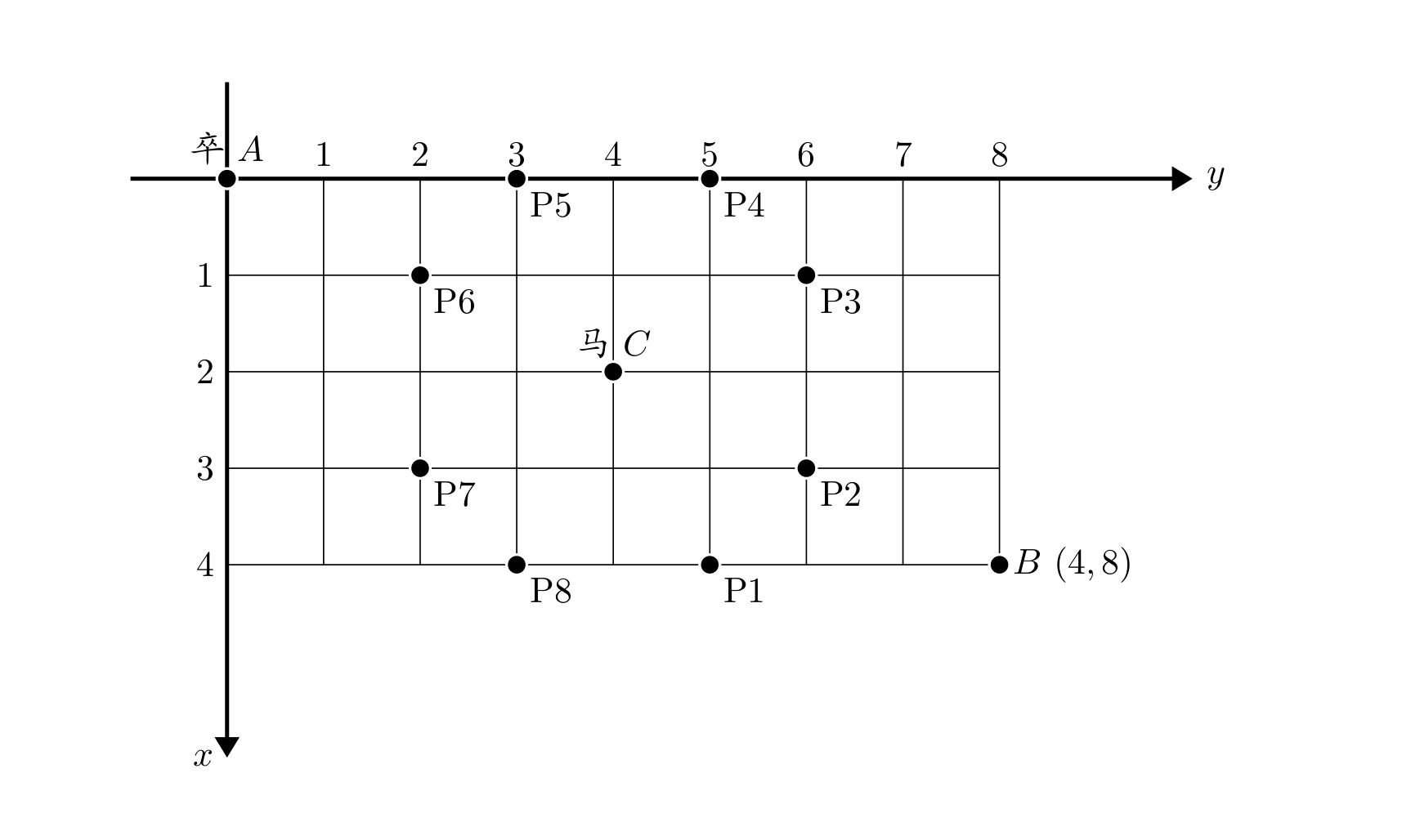
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于 $100 \%$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

解决思路

假如我这个人现在在 $(x,y)$ 这个位置，那么我可以怎么走到这个地方呢？我可以从 $(x-1,y)$ 向右走过来，或者 $(x,y-1)$ 向下走过来。当然第一行只能从左边向右到达，第一列只能从上边向下到达。

这一切的前提是 $(x,y)$ 能够到达（不位于马的控制点）。如果 $(x,y)$ 是马的控制点，那么这个点的路径条数就是 0。

也就是说，人到达 $(x,y)$ 的路径条数，是到达 $(x-1,y)$ 的路径条数，和 $(x,y-1)$ 的路径条数之和。

而初始点 $(0,0)$ 的路径条数为 1，我们就可以得到这样一个转移公式：

$dp_{x,y}=\left\{ \begin{aligned} 0,(x,y) 不能到达\\ 1,x=y=0\\ dp_{i-1,j}+dp_{i,j-1}, 其余情况 \end{aligned} \right.$

为了避免重复计算，可以先根据马的坐标确定八个方向的点分别是哪些点，然后再枚举当前的点是不是这八个点。

当然，马所在的点也是控制点。

AC 代码

#include<iostream>
using namespace std;

long long dp[25][25]; // 存储路径条数
bool no[25][25]; // 存储是不是控制点
int n,m,x,y;
void write_ctrl_pos(int,int); // 标记控制点

int main(){
    cin >> n >> m >> x >> y;
    no[x][y]=true; // 马所在的点一定是控制点
    write_ctrl_pos(x,y); // 标记其他控制点
    dp[0][0]=1; // 原点出发，原点到原点肯定是 1 条路径
    for(int i=0;i<=n;++i){
        for(int j=0;j<=m;++j){
            if(i==0&&j==0)continue; // 跳过原点
            if(!no[i][j]){
                if(i-1<0)dp[i][j]=dp[i][j-1]; // x=0
                else if(j-1<0)dp[i][j]=dp[i-1][j]; // y=0
                else dp[i][j]=dp[i-1][j]+dp[i][j-1]; // 一般情况
            }
        }
    }
    cout << dp[n][m] << endl; // 直接输出最后一条的路径
    return 0;
}

void write_ctrl_pos(int x,int y){
    const int dir[8][2]={{1,2},{1,-2},{2,1},{2,-1},{-1,2},{-1,-2},{-2,1},{-2,-1}}; // 马能控制到的点的各个方向
    for(int i=0;i<8;++i){
        int tx=x+dir[i][0],ty=y+dir[i][1];
        if(tx>=0&&tx<=n&&ty>=0&&ty<=m)
            no[tx][ty]=true;
    }
}

这道题的动态规划的点在于，我们在求解下一个点的路径条数时， 直接调用了上一个点的路径条数，这也是一个比较典型的自底向上的方法。

2. 数字三角形

题目描述

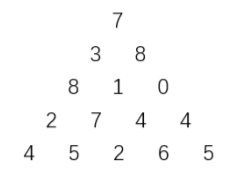
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，走完整个路径后，向左下走的次数与向右下走的次数相差不能超过 1。

输入的第一行包含一个整数 $N (1≤N≤100)$，表示三角形的行数。

下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。
输出描述

输出一个整数，表示答案。

输入输出样例

输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出

27

思路

题目要求走到最后的时候，向左走和向右走的次数的差不超过 1。

也就是说：

1. 如果走了偶数次，那么向左走和向右走的次数相等。如果最后走了偶数次，则这个三角形必然是奇数行，那么最后一行的数字个数也是奇数，最终一定落到最后一行中间的那个数。

2. 如果走了奇数次，那么向左走和向右走的次数一定差 1。如果最后走了奇数次，则这个三角形必然是偶数行，那么最后一行的数字个数也是偶数。最终回落到最后一行中间的两个数，向左走多一点则落在靠左的数，向右走多一点则落在靠右的数。

如果一个三角形有 n 行，对于 第 i 行第 j 个数的路径和的最大值，应该是上一行两个数的路径和的最大值，分别走到这一个数（路径和 +1）的路径和的最大值。由于我们只求最后一行中间的数的路径和，也就是说，我们可以得到：

1. n 为奇数时，这个路径和位于 n 行第 (n+1)/2 的位置。
2. n 为偶数时，这个路径和，是 n 行第 n/2 的位置和 (n+2)/2 的位置的最大值。

由于 C++ 中，对于 int 类型的 / 是整除，当 n 为奇数时，(n+2)/2 和 (n+1)/2 的计算结果是一样的；n 为偶数时，(n+1)/2 的计算结果和 n/2 的计算结果是一样的。

所以我们只需要用 max(c[n][(n+1)/2],c[n][(n+2)/2]) 即可同时涵盖奇数和偶数的情况。

这样，我们就可以逐个计算每个节点的最大路径和，然后一步一步得到最后一行的最大路径和，最后直接输出即可。

AC 代码

#include <iostream>
using namespace std;
int a[101][101],c[101][101];
int main(){
  int n;cin>>n;
  for(int i=1;i<=n;i++)
    for(int j=1;j<=i;j++)
      cin>>a[i][j];
  c[1][1]=a[1][1];
  for(int i=2;i<=n;i++)
    for(int j=1;j<=i;j++)
      c[i][j]=a[i][j]+max(c[i-1][j],c[i-1][j-1]);
  cout<<max(c[n][(n+1)/2],c[n][(n+2)/2]);
  return 0;
}